* 시계열분석
- 시계열 : 변수의 임의의 값들을 시간의 함수로서 표현한 것
주로 (동등한 시간 간격의) 순차적 배열로 표현됨
- 시계열 분석 : 순차적 데이터의 기본 구조와 패턴을 식별, 분석하는 방법론
예측, 모니터링 및 제어 등에 많이 사용됨
* 정상 시계열
- 정상 시계열 : 통계 특성은 시간에 따라 변하지 않는다고 가정한다.
- 엄밀한 통계적 정의는
임의의 변수의 모든 모먼트는(예 : 기대,분산,3차 등) 모든 순간 동일하다.
변수 x의 시간 t와 s에서의 값의 관계를 나타내는 (Xt,Xs)의 합동 분포는 모든시간 r에 대하여 (Xt+r,Xs+r)와 동일하다.
즉, 시간 이동은 중요하지 않다.
* 정상 시계열의 의미
- 각 관측치는 알려지지는 않았지만 예상 상수와 무작위 변동으로 나타난다.

* 이동 평균법
- 단순 이동 평균(SMA) 방법 : 가장 최근 N개의 관측치의 산술 평균을 기반으로 한 예측


* 단순 이동 평균의 장단점
장점
- 쉽게 이해할 수 있다
- 쉽게 계산 됨
- 안정적인 예측 가능
단점
- 데이터의 복잡한 관계를 무시한다.
- 추세에 다소 뒤떨어진다.
과거 N개의 모든 데이터 포인트에 동일한 가중치
따라서 최근 변경 사항의 영향은 즉각적이지 않다.
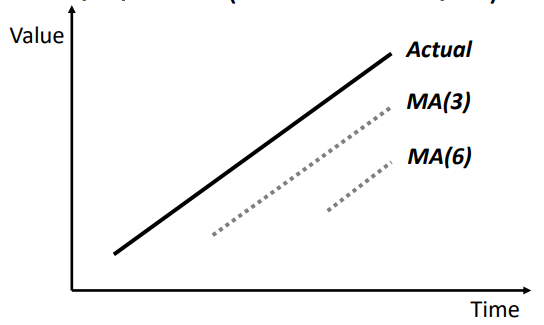
* 추세를 따르는 평균 이동의 지연

* 예측에 대한 이동 윈도우 크기의 영향 (안전성 vs 지연)
* 가중치가있는 이동 평균법
- 단순이동평균법의 단점을 극복하고자 하는 방법 중 하나로, MA계산의 각 요소에 다른 가중치를 부여
-> 가중평균 사용


- WMA에서의 가중치
: 일반적으로 최근 데이터에 더 높은 가중치가 지정됨
: 계절성을 고려할 시, 다른 가중치 패턴 적용 가능
* 지수평활법

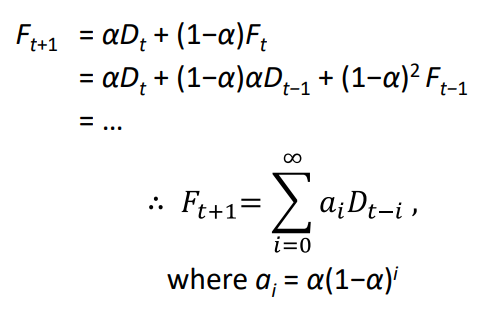
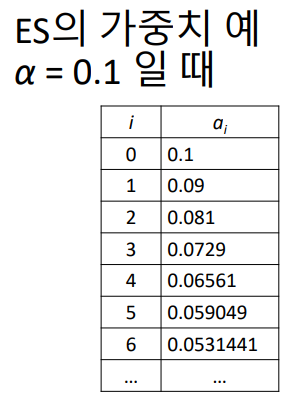
- 지수 평활화 가중치의 크기
: 최근 관측치일수록 상대적으로 더 큼
: 일정한 비율로 (기하학적으로) 감소
- 지수 평활화 가중치의 역할
: 최근 관측치를 상대적으로 더 많이 반영
: 오래된 관측치를 상대적으로 더 적게 반영
- 평활 상수 a의 크기의 영향
: 일반적으로 큰 a는 현재 관찰에 더 많은 가중치 부여
: 패턴의 변화를 빠르게 반영
: 기간별 변동이 큼
- 평활 상수 a 결정
: 기본 평균값이 변경될 가능성이 큰 경우, 상대적으로 큰 값 선택한다.
: 기본 평균값이 안정될 가능성이 큰 영우, 상대적으로 작은 값을 선택한다.
: a는 일반적으로 운영관리 응용 분야의 예측 안정성을 위해, 큰 값을 취하지는 않는다.
- 평활 상수 a 결정 방법
: 흔히 0.1 ~ 0.3 정도가 많이 선택된다.
: 최적 a값을 구하는 수학적 방법론 존재한다.
- 초기 예측
: ES를 처음 사용하는 경우, 시작 시점의 예측값이 필요하다.
: 하지만, 초기 예측값은 존재하지 않아, 초기 예측치를 다른 값으로 대체하여 사용한다.
- 초기 예측을 대체하는 값
: 관측값 데이터 그 자체를 사용
: 여러 기간의 평균으로 설정
: 초기 기간 동안 다른 예측 방법을 사용
- 초기 값의 영향
: 초기 값은 초기 예측에는 큰 영향을 준다.
: 그 영향은 결국은 점점 작아진다.
* 단일, 이중, 삼중 지수 평활법
- ES에는 단일, 이중 및 삼중 지수 평활법이 존재한다.
- 단일 지수 평활법 : 추세나 계절성이 없을 경우
- 이중 지수 평활법 : 추세가 존재할 때
- 삼중 지수 평활법 : 추세와 계절성이 존재할 때
'생산운영관리' 카테고리의 다른 글
| [생산운영관리] 계절성이 있는 수요 분석 (0) | 2024.05.04 |
|---|---|
| [생산운영관리] 추세 고려하는 예측 방법(회귀 분석, 이중 지수 평활법) (0) | 2024.04.28 |
| [생산운영관리] 예측의 분류와 예측 모델 (0) | 2024.04.27 |
| [생산운영관리] 예측, 수요예측에 대하여 (1) | 2024.04.27 |
| [생산운영관리] 생산운영관리의 의사결정 (0) | 2024.03.18 |



