* 최소 제곱 추정
: y와 y^ 간의 차이에 대한 제곱의 합을 최소화 함
: 즉 에러 𝝐, 에 대한 제곱의 합을 최소화하는 𝜷를 추정함
yi = B0 + B1*Xi + Ei
y^i = B0 + B1*Xi
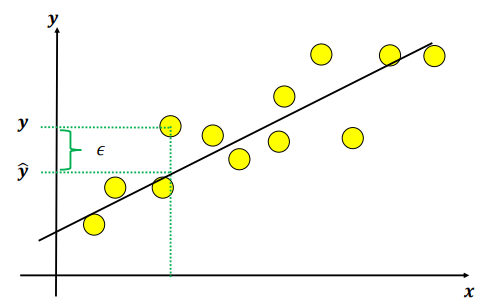
※ SSE = Sum of Squared Error / MSE = Mean SSE

* 에러 제곱의 합
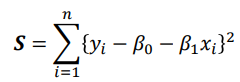
𝛽0 및 𝛽1에 대한 편미분은 다음과 같음:
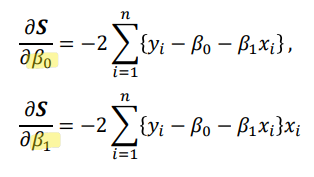
* 정규식
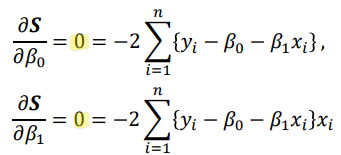
이를 통해 구할 수 식은 아래와 같습니다. : 이를 정규 식(Normal Equation)이라고 함
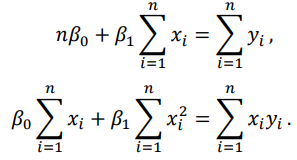

계수 𝛽^(혹은 𝒃’s)들은 회귀 파라미터(parameter) 𝛽의 최소 제곱 추정에 의해 값을 정함
그러면 한번 예제 문제를 풀어보도록 하겠습니다!

1. X와 Y의 평균을 구한다.
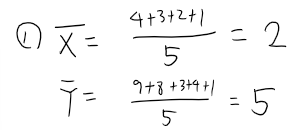
2. B0와 B1의 값을 구한다.
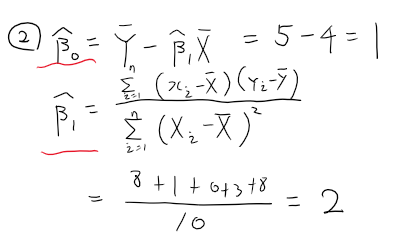
3. Y^ 값을 구한다.
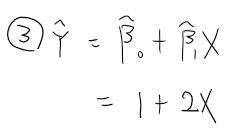
4. Ei 값을 구한다.
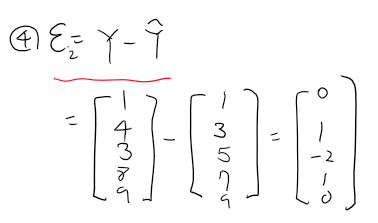
5. Ei의 제곱을 구한다.
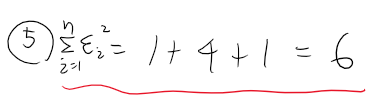
* 행렬 형태의 최소 제곱 추정 구하기 : Y=XB+E
- 에러 제곱 합은 다음과 같이 표현할 수 있음
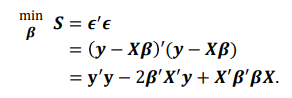

이번에도 예제를 풀어보면서 이해해보겠습니다!

1. Design Matrix를 만듭니다.
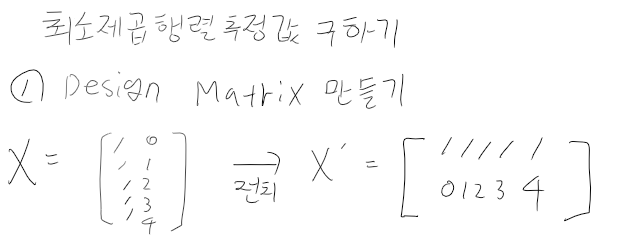
2. XX'의 역행렬을 구합니다.
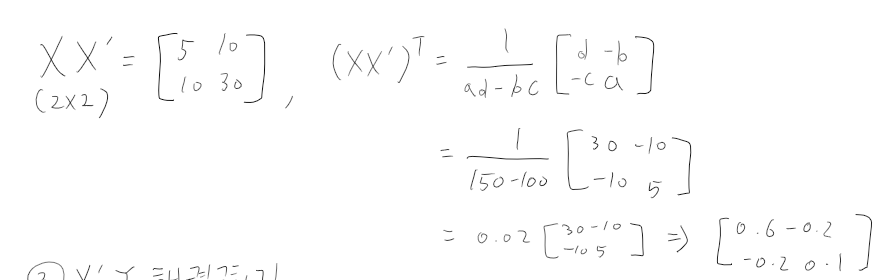
3. X'Y 행렬을 구하기
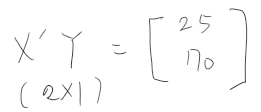
4. B^을 구하기
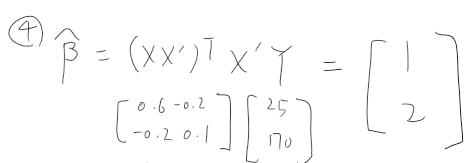
5. Y^을 구하기

6. E을 구하기

7. E'E을 구하기 -> 에러 제곱의 합을 구하기

'데이터마이닝' 카테고리의 다른 글
| [데이터마이닝] 모델 진단(잔차산점도, 이상치 발생, QQ산점도) (0) | 2024.04.24 |
|---|---|
| [데이터마이닝] 회귀 모델 적합도 측정 (0) | 2024.04.22 |
| [데이터마이닝] 회귀 분석에 대하여 (0) | 2024.04.19 |
| [데이터마이닝] 가설 검정과 상관 관계에 대하여 (0) | 2024.04.19 |
| [데이터 마이닝] 피어슨(pearson) 상관 분석에 대하여 1_상관행렬 구하기 (0) | 2024.03.28 |



