* 정보이론
- 사람이 어떻게 정보를 처리하는지 연구하려면 정보라는 용어의 실무적 정의와 측정 방법이 있어야 한다.
- 정보이론에서는 정의와 정량적 측정방법을 배운다.
* 정보의 개념
- 정보이론에서 정보란 불확실성의 감소라 정의한다.
- 정보는 줄이는 것이 좋다. 정보가 0인게 좋다.
- 정보의 정의에서는 메시지 자체의 중요성은 직접 고려하지 않는다. 그 출현 가능성만을 고려한다.
- 확실한 사건의 출현에는 정보의 양이 적다.
- 아주 불확실한 사건에는 많은 정보가 담겨있다.
ex) 이미 확실한 것은 정보가 없는 것이고, 불확실한 것은 사람이 생각을 많이 해야 하니 정보가 많은 것
자동차의 엔진온도 경고등이 들어왔다 -> 의심스러운 사건으로 많은 정보가 담겨 있다.
안전띠 착용 경고 -> 중요하지만 자동차가 출발할 때마다 나타나므로, 정보이론에서는 정보를 거의 가지고 있지 않다.
* 정보 측정단위
- 정보이론에서 정보를 bit 단위로 측정
- 1 bit는 일어날 가능성이 동일한 두 대안에서 하나를 결정해야 할 때 필요한 정보의 양
- 여러 대안의 확률이 동일하고 이러한 대안의 수가 N이라면, 정보량 H[bit]는 밑이 base 2인 로그와 같다.
H = log2^N
- 대안이 두 가지 뿐이면, 정보는 1 bit 이다. => log2^2 = 1
- 네 가지 동일한 대안의 정보량은 2 bits 이다. => log2^4 = 2
- 0~9의 수의 집합에서 무작위로 선택한 숫자가 전달하는 정보량은 3.322bits (log2^10)
- A~Z의 문자 집합에서 무작위로 선택한 문자가 가지는 정보는 4.7bits 이다. (log2^26)
다양한 자극 차원에 대해 인간이 만들 수 있는 절대적 구분(차이 인지)의 평균 횟수와 그에 해당하는 비트 수를 보여줍니다. 자극 차원은 다음과 같습니다:
- 순수 음조(Pure tones) - 평균 구분 횟수: 5회, 전달된 비트 수: 2.3 비트
- 음량(Loudness) - 평균 구분 횟수: 4-5회, 전달된 비트 수: 2-2.3 비트
- 시각적 객체의 크기(Size of viewed objects) - 평균 구분 횟수: 5-7회, 전달된 비트 수: 2.3-2.8 비트
- 밝기(Brightness) - 평균 구분 횟수: 3-5회, 전달된 비트 수: 1.7-2.3 비트
- 대안의 출현 가능성이 동일하지 않을 때는 한 사건이 가진 정보를 다음 공식으로 구한다.
h(i) = log2^1/p(i)
- 확률이 다른 일련의 사건이 가지는 평균 정보량은 다음 식으로 계산한다.
ex) 적군이 육지나 바다로 침략할 확률이 각각 0.9 및 0.1이라면, 평균 정보량은?

- 대안의 출현 가능성이 같으면 가능한 최대의 정보량이 된다.
- 즉, 적군의 침략 신호의 최대 기능 정보량은? => 1.0
- 서로의 확률이 같지 않을수록 정보량은 그만큼 최대량에서 줄어든다. (예시 참고)
- 여기서 중복률의 개념이 생기는데, 이것은 출현 확률이 같지 않기 때문에 최대치로 부터 정보량이 감소하는 양이다.

- 중복률은 다음과 같은 식으로 계산한다.

- 통신채널의 대역폭이라는 개념은 정보의 전달속도를 초당 bit(bit/s)로 측정한 것이다.
- 귀의 대역폭은 8000~10000 bit/s 이고, 눈은 1000bit/s으로 추산된다.
- 이 정보량은 뇌에서 흡수하고 해석할 수 있는 양보다 많기 때문에 말초 감각기관에서 수용된 정보는 뇌에 도달하기 전에 대부분이 여과된다.
* 정보이론의 응용
1) Bishu and Drurys는 배선작업에서 bit 단위로 측정한 정보량을 사용하여 작업 완수시간을 추정
- 정보량은 골라야 하는 전선의 수와 전선을 연결할 단자 수의 함수였다.
- 즉 작업시간은 그 작업에 관계되는 정보량과 선형관계가 있음 -> 많으면 정보가 많아지고 결국 작업시간이 선형으로 늘어난다.
2) 힉-하이만의 법칙 : 선택반응시간은 자극 정보와 선형관계에 있다.
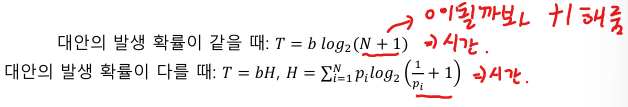
T 는 선택반응시간(CRT),
b는 실험에 의해 측정된 상수,
N은 대안의 수,
pi는 대안의 발생 확률 대안이 0개일 때 로그값을 0을 만들기 위해 1 더함,
대안이 1개일 때 로그값이 1이므로 b시간 소요됨